Ng Chu Ming (黄祖铭)

B.Eng in Computer Engineering (2nd Upper), National University of Singapore
M.Sc in Computer Science (by Research), National University of Singapore
M.Sc in Mathematical Finance (with Distinction), University of Oxford

   We have no history, but we have a rendezvous with destiny...

- Maj. Gen. William C. Lee (101st Airborne)   

Chu-Ming is a Singaporean chinese and is currently Core Strategist, Vice President with the CIB Core Strategies Group in JPMorgan Chase & Co. Inc. The Core Strategies Group is a quant developer group working in foreign exchange, commodities, emerging markets, and mortgages. The group covers the market making businesses, mainly on the derivatives side, though also in foreign exchange electronic market making and hedging algorithms. We build the trading and risk management platform Athena (see also Risk magazine on Athena ).

Prior to JPMorgan he was Associate Director with UBS Investment Bank where he was development lead for it's inhouse electronic trading and smart order routing system for equities trading based on UBS Pinpoint technology.

Before joining UBS he was Analytics / Pricing developer in Electronic Trading Technology with investment bank Merrill Lynch & Co. Inc. His work in Merrill spans the design and architecture of timeseries/bitemporal databases and also quantitative analytics using the vector processing language Q. Notable work done in Merrill include the proof of concept implementation of integrating Q with Nvidia's CUDA API, bringing 6-8x performance gains in analytics such as full day VWAP computation. He also worked on the design of multithreaded Java Analytics API for algo trading engines. In this area he introduced Google's MapReduce inspired distributed processing, improving full day VWAP for the entire US equities universe by 5x.

Before joining Merrill, he has experience in large scale software development during his tenure as Software Development Engineer with Autodesk Inc working on the Vault-Addin, which is part of the flagship AutoCAD drafting software.

He received his Bachelor's degree in Computer Engineering (2nd Upper Hons) and M.Sc. (by Research) in Computer Science from the National University of Singapore, as well as a M.Sc in Mathematical Finance (with Distinction) from the University of Oxford. During his MSc with NUS, he also held position as Research Staff with the School of Computing working on algorithms and data structures for automatic design generation of architectural forms. See a demo video here, here for various features of the software suite. In the quantitative finance domain, he is previleged to have worked with Riccardo Rebonato on stochastic volatility models which straddles the P- and Q- measures, with the aim of applying them to the analysis of market-price-of-volatility risk. In terms of academic research, he is one of the few who has published both in computer science and in the quant finance domain (see more in publications section).

Chu-Ming's broad interests include Computer Graphics and Visualization, Computational Geometry, as well as data structures and theoretical aspects of computer science. He is also interested in algorithmic problem solving. Specific areas of interests and expertise include out-of-core terrain visualization, surface reconstruction, geometric algorithms, spatial data structures as well as automatic design generation of building forms. He is also experienced in large scale C++ software development, design patterns, OOAD from his experience working with the 25 years, 9 million lines code base of AutoCAD.

With his venture into the finance he now takes an active interest analytics and quantitative methods in finance. This curiosity was partly kindled by the story of Long Term Capital Management.

During his younger days, he took a passionate interest in the art and lore of Demo Coding.

His other interests outside of academia includes wushu, inline skating, bike tricks.

He is also into long distance running and successfully completed a full distance marathon in the Standard Chartered Singapore Marathon 2006

In his past life, he also served as a paratrooper with the 1st Commando Battalion, Singapore Armed Forces. 

Quick Links

Publications

  • A Financially Motivated Extension of the Heston Model for a Joint P- and Q-Dynamics Analysis of Variance
    Riccardo Rebonato, Chu-Ming Ng
    The Journal of Derivatives, Spring 2018, 25 (3) 55-80.
  • Growing Non-Regular Architectural Forms. (Technical Report)
    Chu-Ming Ng, Tiow-Seng Tan, Joseph Lim, Yenn-Jin Ho, Wai-Heng Lai
    See the project website for some preliminary info and a demo video here
  • Analyzing Prefetching in Large-Scale Visual Simulation pdf
    Chu-Ming Ng, Cam-Thach Nguyen, Dinh-Nguyen Tran, Shin-We Yeow, Tiow-Seng Tan
    Proceedings of The Computer Graphics International 2005,     22-24 June, Stony Brook, New York, USA, pp. 100--107.
    See project website for more information.
  • Analyzing Prefetching in Large-Scale Visual Simulation
    Chu-Ming Ng, Cam-Thach Nguyen, Dinh-Nguyen Tran, Shin-We Yeow, Tiow-Seng Tan
    ACM SIGGRAPH 2005 Symposium on Interactive 3D Graphics and Games, Washington D.C., USA
  • Prefetching in Visual Simulation pdf
    Chu-Ming Ng, Cam-Thach Nguyen, Dinh-Nguyen Tran, Shin-We Yeow, Tiow-Seng Tan
    Proceedings of IEEE Visualization 2003, Seattle, Washington, USA

     I have Erdos Number 4. (Paul Erdos->Aronov Boris->Herbert Edelsbrunner->Tiow-Seng Tan-> Chu-Ming Ng)

Talks 

  • "Demos and Real-time Computer Graphics"
    Talk given to the Computer Graphics Research Lab, School of Computing, NUS, (23rd March'09)
    Feel free to use the slides

  • "Bringing Color to the world of Finance / Time Series Analytics".
    Talk given to 60+ local audience in Merrill Lynch and broadcast to several other Asian geographies. Covers the use of NVIDIA graphics processors (GPU) for financial computation using the CUDA API. Particular focus on integrating CUDA with KDB+/Q seamlessly to achieve 6-8x performance improvement over the already blazingly fast Q language.

Research Interests

Computational geometry, computer graphics, terrain visualization, architecture form generation.

I love computational geometry and in my free time I enjoy thinking about shapes and their application to graphics. My greatest fascination is with Dual space algorithms such as the Dual Space algorithm for solving the Stabbing line segment problem, as well as the lifting transformation for computing 2D Delaunay Triangulation via lifting it up to 3 dimensions. Taking things up one additional dimension sometimes provide a new dimension of insights, such as that for Moebius Transformations.

"There is some magic to geometric transformations which has to do with the way humans understand geometric problems. Even though it is fairly obvious that the transformation of one problem into another cannot lead to anything new(with respect to computational complexity), in particular if the transform realizes a one-to-one correspondence.

Nevertheless, there is an impressively large collection of geometrical problems whose tranformation into other problems play a crucial role in their resolution.

The intuitive explanation is perhaps that transformations shift the emphasis of the problem to other aspects that are not as readily apparent in the original problem, thus facilitating the study of the problem from a new angle.

A prime example that substantiates this interpretation is the dual transform that maps a point to a hyperplane. This is as simple as interpreting the coordinates of a point as coefficients of a plane equation. Interestingly, when applying this transformation to point sets in Rd, the angles determined by small subcollections of the set "materialize" into faces in the dual arrangement. Thus, duality help us in understanding the otherwise not very intuitive concept of angles..."

Herbert Edelsbrunner 

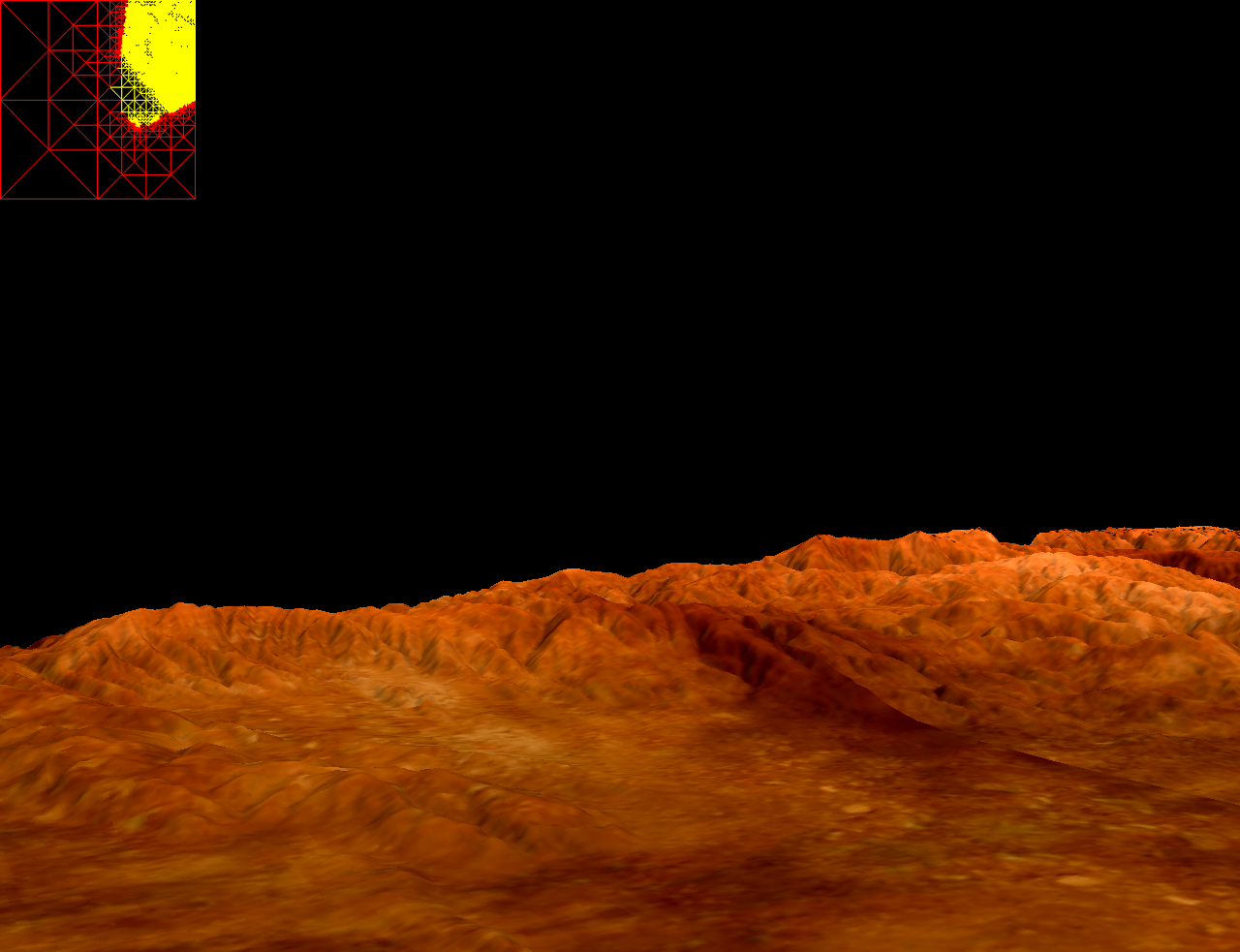
Terrain Visualization (dyanamic level of detail for terrain walkthrough, based on ROAM) 

  

Screenshots of the level of detail terrain engine with multitexturing of terrain textures.

     

Illustration of dynamic tessellation of terrain geometry as the view point changes. Notice that the regions in-view (shown in yellow) are more highly tesselated. Similarly, flat regions are less tesellated to save triangle budget. The rectangular grid in the top left of each image shows a top down view of the terrain geometry from frame to frame.